درک الگوریتم سینوس-کسینوس (SCA) برای بهینه سازی در MATLAB
درک الگوریتم سینوس-کسینوس (SCA) برای بهینه سازی در MATLAB
الگوریتم سینوس-کسینوس (SCA) یک الگوریتم بهینه سازی فراابتکاری ست که از حرکت دوره ای توابع سینوس و کسینوس الهام گرفته است. این یک ابزار قدرتمند برای حل مسائل بهینه سازی پیچیده در MATLAB است. در این پاسخ، به جنبه های کلیدی SCA و پیاده سازی آن در MATLAB می پردازیم.
درک الگوریتم سینوس-کسینوس (SCA)
الگوریتم سینوس-کسینوس یک تکنیک بهینه سازی مبتنی بر جمعیت است که رفتار دوره ای توابع سینوس و کسینوس را تقلید می کند تا فضای جستجو را اکتشاف کرده و بهینه جهانی را پیدا کند. الگوریتم جمعیتی از راه حل های کاندید را تولید می کند و سپس به صورت دورهای موقعیت این راه حل ها را بر اساس توابع سینوس و کسینوس به روز می کند.
مراحل اصلی الگوریتم SCA به شرح زیر است:
1. مقداردهی اولیه : الگوریتم با ایجاد جمعیتی از راه حل های کاندید شروع می کند، که هر راه حل به صورت یک بردار متغیرهای تصمیم نشان داده می شود.
2. به روز رسانی موقعیت : در هر تکرار، الگوریتم موقعیت هر راه حل کاندید را با استفاده از معادلات زیر به روز می کند:
```
x_new = x_current + r1 * sin(r2) * |r3 * p_best - x_current|
y_new = y_current + r1 * cos(r2) * |r3 * p_best - y_current|
```
در اینجا، `r1`، `r2` و `r3` اعداد تصادفی بین 0 و 1 هستند و `p_best` بهترین موقعیت شخصی راه حل فعلی است.
3. ارزیابی و گزینش : الگوریتم تابع هدف را برای هر راه حل به روزرسانی شده ارزیابی می کند و بهترین راه حل ها را برای انتقال به تکرار بعدی انتخاب می کند.
4. شرط توقف : الگوریتم به تکرار ادامه می دهد تا زمانی که یک شرط توقف مشخص مانند حداکثر تعداد تکرارها یا یک مقدار تابع هدف هدف برآورده شود.
پیاده سازی الگوریتم سینوس-کسینوس در MATLAB
برای پیاده سازی الگوریتم سینوس-کسینوس در MATLAB، می توانید از این مراحل کلی پیروی کنید:
1. تعریف تابع هدف : یک تابع MATLAB بنویسید که تابع هدفی را که می خواهید بهینه سازی کنید، نشان می دهد.
2. مقداردهی اولیه جمعیت : یک جمعیت از راه حل های کاندید ایجاد کنید، جایی که هر راه حل به صورت یک بردار متغیرهای تصمیم نشان داده می شود.
3. پیاده سازی به روز رسانی موقعیت : موقعیت هر راه حل کاندید را با استفاده از معادلات سینوس-کسینوس ارائه شده قبل به روز کنید.
4. ارزیابی تابع هدف : تابع هدف را برای هر راه حل به روزرسانی شده ارزیابی کرده و بهترین راه حل ها را انتخاب کنید.
5. تکرار فرآیند : مراحل به روزرسانی موقعیت و ارزیابی را تا زمانی که شرط توقف برآورده شود، تکرار کنید.
این یک مثال پیاده سازی الگوریتم سینوس-کسینوس در MATLAB است:
```matlab
function [best_solution, best_value] = sca_optimization(objective_function, num_variables, num_solutions, max_iterations)
% مقداردهی اولیه جمعیت
population = rand(num_solutions, num_variables);
% مقداردهی اولیه بهترین راه حل و بهترین مقدار
best_solution = population(1, :);
best_value = objective_function(best_solution);
% تکرار تا زمانی که شرط توقف برآورده شود
for i = 1:max_iterations
% به روزرسانی موقعیت هر راه حل
for j = 1:num_solutions
x_new = population(j, 1) + rand * sin(rand) * abs(rand * best_solution(1) - population(j, 1));
y_new = population(j, 2) + rand * cos(rand) * abs(rand * best_solution(2) - population(j, 2));
population(j, :) = [x_new, y_new];
end
% ارزیابی تابع هدف و به روزرسانی بهترین راه حل
for j = 1:num_solutions
current_value = objective_function(population(j, :));
if current_value < best_value
best_solution = population(j, :);
best_value = current_value;
end
end
end
end
```
در این مثال، تابع `sca_optimization` یک تابع هدف، تعداد متغیرهای تصمیم، تعداد راه حل های در جمعیت و حداکثر تعداد تکرارها را به عنوان ورودی می گیرد. سپس جمعیت را مقداردهی اولیه می کند، موقعیت راه حل ها را به روز می کند، تابع هدف را ارزیابی می کند و در هر تکرار بهترین راه حل و بهترین مقدار را به روز می کند.
می توانید از این تابع برای بهینه سازی هر تابع هدف در MATLAB با ارسال آن به عنوان یک آرگومان به تابع `sca_optimization` استفاده کنید.
بهینه سازی توابع با الگوریتم سینوس-کسینوس
الگوریتم سینوس-کسینوس ابزار قدرتمندی برای حل طیف گسترده ای از مسائل بهینه سازی در MATLAB است، از جمله:
- مسائل بهینه سازی بدون محدودیت
- مسائل بهینه سازی با محدودیت
- مسائل بهینه سازی چندهدفه
- مسائل بهینه سازی جهانی
SCA به ویژه برای حل مسائل بهینه سازی پیچیده، غیرمحدب و چندحداکثری مفید است، که در آن روش های مبتنی بر گرادیان ممکن است در پیدا کردن بهینه جهانی دچار مشکل شوند.
با بهره گیری از رفتار دوره ای توابع سینوس و کسینوس، SCA قادر است فضای جستجو را به طور موثرتری اکتشاف کرده و از گیر افتادن در بهینه های محلی اجتناب کند. این آن را به یک افزونه ارزشمند به جعبه ابزار بهینه سازی MATLAB تبدیل می کند و با سایر الگوریتم ها مانند الگوریتم ژنتیک، بهینه سازی تکامل ازدحامی ذرات و شبیه سازی سرد تکمیل می کند.
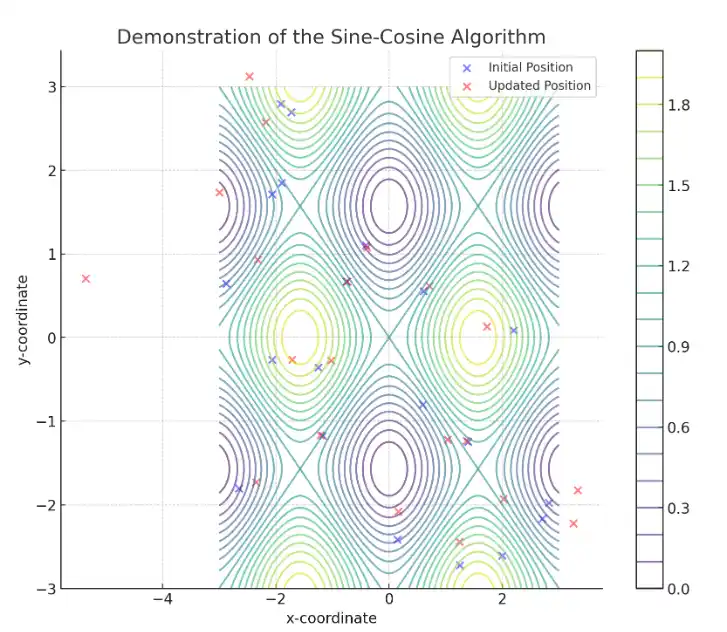
تصویر بالا نمایشی از الگوریتم سینوس-کسینوس است. در این تصویر، نقاط آبی رنگ موقعیت اولیه جمعیت راه حل های کاندید را نشان می دهند و نقاط قرمز رنگ نشان دهنده موقعیت به روزرسانی شده آن ها پس از یک تکرار الگوریتم هستند. نمودار همچنین شامل خطوط کانتور است که مقادیر تابع هدف را در فضای دو بعدی نشان می دهد، کمک کننده برای درک بهتر فرآیند بهینه سازی و جهت گیری حرکت راه حل ها به سمت مناطق با ارزش بهتر تابع هدف است.
امیدوارم این مقدمه بر الگوریتم سینوس-کسینوس و پیاده سازی آن در MATLAB مفید بوده باشد.
https://Bahrambeigi.work
https://g.dev/yousefbahrambeigi